- Генератори випадкових чисел
- Навіщо мені може знадобитися конкретне число з послідовності?
- Чи можу я просто використовувати ГСЧ з різними значеннями сида?
- Випадкові хеш-функції
- Оптимізація хеш-функцій для процедурної генерації
- Комбінування хеш-функцій і ГСЧ
- висновок
- Додаток A: Примітка з тривалого шуму
- Додаток B: Результати додаткових тестів
- Чи не краще використовувати в якості сида великі значення?
- ГСЧ потрібно зробити кілька значень, щоб «розігнатися»?
- Правда, що деякі ГСЧ, наприклад в Java, видають кращу випадковість чисел з послідовностей з різними сидами?
- Чому для випадкових хеш-функцій можна використовувати різні сиди, а для ГСЧ не можна?
- Додаток C: Додаткове порівняння хеш-функцій
Створюючи щось процедурне, ви практично гарантовано зіткнетеся з необхідністю застосування випадкових чисел. І якщо ви захочете, щоб один і той же результат видавався більше одного разу, вам будуть потрібні повторювані випадкові значення.
У цій статті в якості прикладів буде використовуватися генерація ігрових рівнів / світів, але ці уроки можна застосувати й до таких речей як процедурні текстури, моделі, музика і т.д. Однак, це не стосується областей з чітко визначеними вимогами, на кшталт криптографії.
Навіщо може знадобитися повторювати один і той же результат?
- Можливість заново відвідати той же рівень / світ. Наприклад, певний рівень / світ створюється з специфічного сида. Використовуючи той же сид, ви знову отримаєте той же рівень / світ. Це можна зробити, наприклад, в Minecraft .
- Постійний світ, що генерується на льоту. Коли світ генерується по ходу того як його вивчає гравець, може знадобитися, щоб вже відвідані локації залишалися колишніми (як в Minecraft або прийдешньої No Man's Sky), а не змінювалися кожен раз, як уві сні.
- Один світ для всіх. Ймовірно, ви захочете, щоб світ був однаковим для всіх гравців, як ніби він не був згенерований процедурно. Саме так і влаштована No Man's Sky. Тут майже як і у випадку з поверненням в відвіданих рівень / світ, крім того моменту, що завжди використовується один сид.
Ми кілька разів згадали слово «сид». Сідом (seed) може бути число, текстовий рядок, або інші дані, що використовуються як вхідний значення для отримання випадкового результату на виході. Відмінною рисою сида є те, що один і той же сид завжди видає однаковий результат, але навіть найменше його зміна може привести до зовсім іншого результату.
У цій статті ми розглянемо два різні способи отримання випадкових чисел - генератори випадкових чисел і випадкові хеш-функції - і причини для вибору одного або іншого. Ці знання далися мені непросто, і подібну інформацію складно знайти у вільному доступі, так що я вирішив, що просто зобов'язаний написати цю статтю і поділитися нею.
Генератори випадкових чисел
Найбільш простим способом отримання випадкових чисел є генератори випадкових чисел, або ГВЧ. У багатьох мовах програмування є класи і методи ГВЧ зі словом random в назві, так що вони будуть очевидною відправною точкою.
Генератор випадкових чисел видає послідовність випадкових значень в залежності від вихідного сида. В об'єктно-орієнтованих мовах ГСЧ - це зазвичай об'єкт, не започатковано за допомогою сида. Після цього метод об'єкта може повторно викликатися для генерації випадкових чисел.
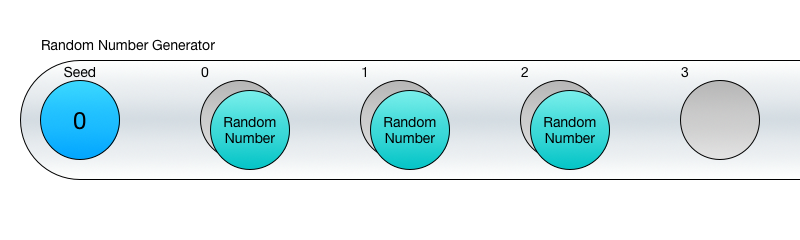
Код на C # буде виглядати приблизно так:
Random randomSequence = new Random (12345);
int randomNumber1 = randomSequence.Next ();
int randomNumber2 = randomSequence.Next ();
int randomNumber3 = randomSequence.Next ();
В даному випадку ми отримуємо випадкове ціле число від 0 до максимально можливого цілого (2147483647), але вам не важко буде призначити результатом випадкове ціле число з потрібного діапазону або випадкове число з плаваючою комою від 0 до 1. Є чимало методів, що роблять це самостійно.
Ось зображення перших 65536 чисел, згенерованих класом Random в C # з сида 0. Кожне число представлено пикселем з яскравістю від 0 (білий) до 1 (чорний).

Тут важливо розуміти, що ви не зможете отримати третій випадкове число, поки не отримаєте перше і друге. Це не просто недогляд в реалізації, така сама суть ГСЧ - він генерує кожне нове число, використовуючи попереднє в своїх обчисленнях. Тому ми і говоримо про випадкову послідовність.
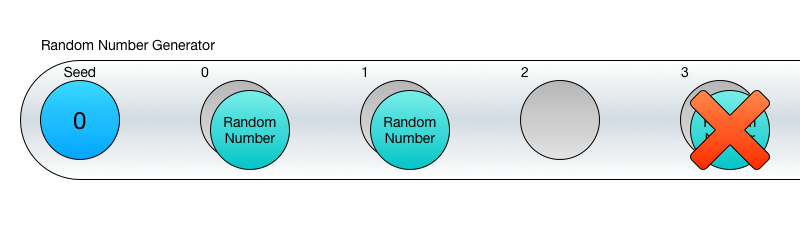
Це означає, що поки вам потрібно кілька йдуть по порядку випадкових чисел, то ГСЧ відмінно з цим впораються, але якщо потрібно конкретне значення (скажімо 26-е за рахунком), то тут вам не пощастило. Ну, ви, звичайно, можете 26 разів викликати Next () і використовувати останнє число, але це погана ідея.
Навіщо мені може знадобитися конкретне число з послідовності?
Якщо ви генеруєте все і відразу, то такі значення вам, можливо, і не знадобляться, принаймні я не зможу придумати для цього причину. Інша справа, якщо щось генерується на льоту і по частинах.
Скажімо, у вас є три секції ігрового світу: A, B, і C. Гравець починає в секції A, вона генерується за допомогою 100 випадкових чисел. Потім гравець просувається в секцію B, яка генерується 100 інших випадкових чисел. В цей же час секція A знищується, звільняючи місце в пам'яті. Далі йде секція C, для створення якої використовуються інші 100 значень і також видаляється секція B.
Однак, якщо гравець захоче повернутися в секцію B, її потрібно генерувати з тих же значень, що і в перший раз, щоб вона виглядала незмінною.
Чи можу я просто використовувати ГСЧ з різними значеннями сида?
Ні! Це досить поширеною оману. Суть в тому, що числа однієї послідовності випадкові по відношенню один до одного, але числа того ж порядку з різних послідовностей випадковими по відношенню один до одного не будуть, навіть якщо так і здасться на перший погляд.
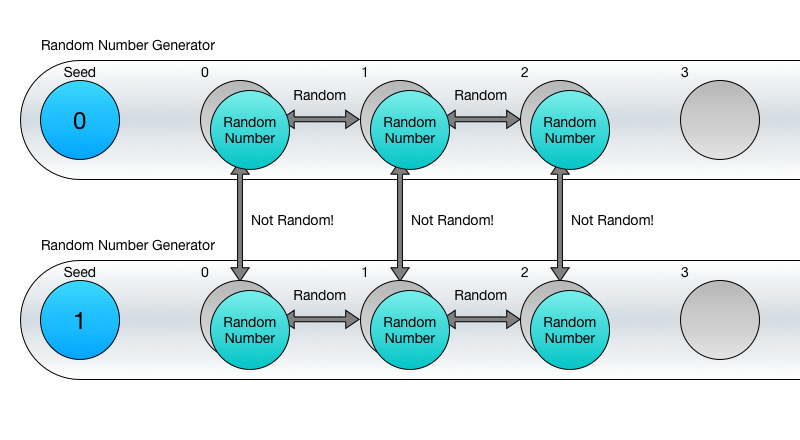
Так що, якщо взяти перші числа з 100 послідовностей, вони не будуть випадковими по відношенню один до одного. Та ж картина буде спостерігатися і з 10-ми, 100-ми або 1000-ми порядковими значеннями послідовностей.
До цього моменту багато поставляться скептично, і це нормально. можете ознайомитися з цим питанням на Stack Overflow , Якщо це сильніше вас переконає. Але ми з вами виберемо дещо цікавіше і поінформатівнее і трохи поекспериментуємо.
Давайте порівняємо знайому нам послідовність з першими числами з 65536 послідовностей, згенерованих з сидов від 0 до 65535.
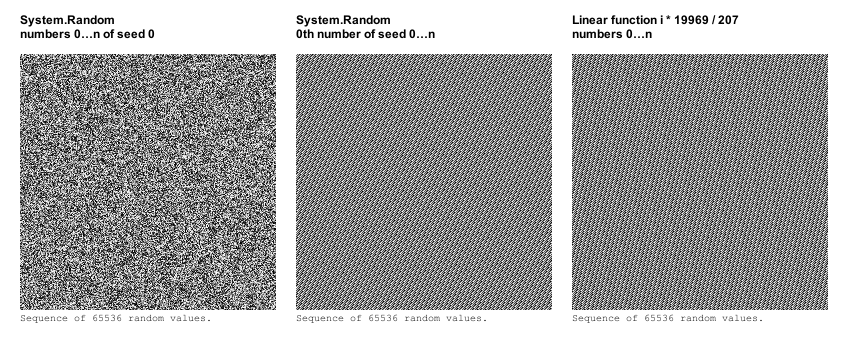
Візерунок досить рівномірно розподілений, але він не зовсім випадковий. Для порівняння я розмістив поруч результати з абсолютно лінійної функції, і видно, що послідовні сиди видають числа, по випадку не далеко пішли від роботи простий лінійної функції.
Так адже вони майже випадкові? Цього ж буде досить?
Настав час представити вам способи більш точного вимірювання випадковості, тому що не варто довіряти визначенню на око. Але навіщо? Хіба результат не виглядає досить випадковим?
В общем-то так, наша кінцева мета досить достовірно зобразити випадковість. Але випадкові числа можуть зовсім по-різному виглядати на виході, в залежності від області їх застосування. Ваші алгоритми генерації можуть трансформувати випадкові значення будь-якими способами, виявляючи чіткі закономірності, непомітні при простому погляді на впорядковану послідовність.
Альтернативним способом перевірки випадковості результату є створення 2D-координат з спарених випадкових чисел і побудова зображення за цими координатами. Чим більше координат потрапляє на один і той же піксель, ті яскравіше він стає.
Давайте поглянемо на зображення, отримані таким чином для звичайної послідовності і для чисел, узятих з різних послідовностей з різними сидами. Так, і ще додамо ту лінійну функцію.
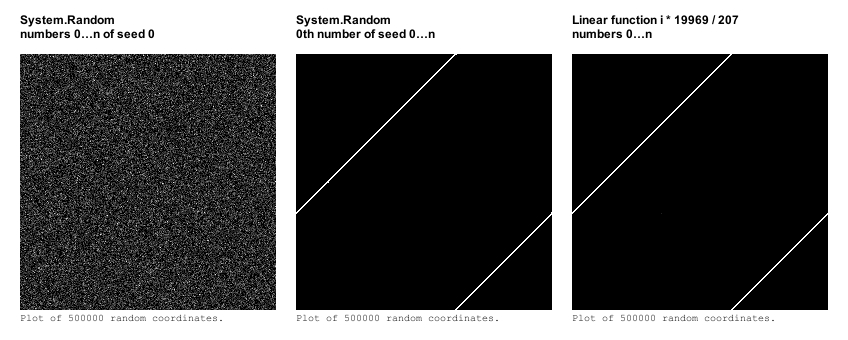
Кого-то, ймовірно, здивує, що координати з послідовностей з різними сидами шикуються в тонкі прямі лінії, що вже зовсім не назвати рівномірним розподілом. І лінійна функція знову видає схожий результат.
Уявіть, що ви генеруєте координати для посадки дерев. Всі вони будуть збудовані в прямі ряди, а інша місцевість залишиться порожньою!
Можна зробити висновок, що ГВЧ знадобляться, тільки якщо вам не потрібен доступ до порядковим значенням послідовностей. В іншому випадку варто звернути увагу на випадкові хеш-функції.
Випадкові хеш-функції
Хеш-функція - це, простіше кажучи, будь-яка функція для відображення даних довільного обсягу у вигляді даних фіксованого обсягу, де невелика різниця в початкових значеннях перетвориться в велику різницю на виході.
Основне використання в процедурній генерації - надання одного або декількох цілих чисел в якості вхідних даних і отримання випадкового значення в якості результату. Наприклад, у великих світах, де за один раз генерується тільки мала їх частина, основна необхідність - отримання випадкового числа, пов'язаного з вхідним вектором (таким, як ігрова локація), так щоб це число завжди залишалося незмінним при незмінному вхідному значенні. На відміну від ГСЧ, тут немає послідовностей - числа можна отримувати в будь-якому бажаному порядку.
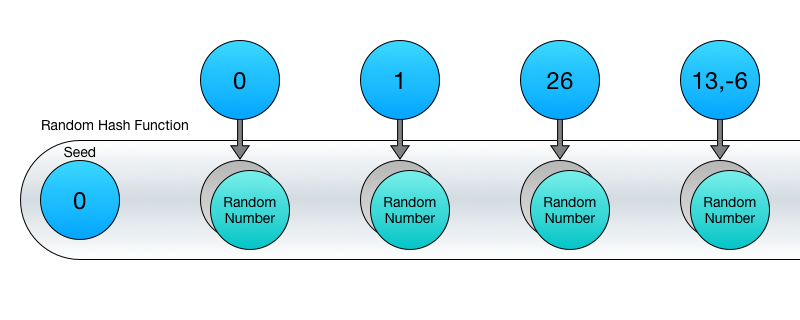
Код на C # буде виглядати приблизно так - зверніть увагу, що ви можете довільно вказувати порядок значень:
RandomHash randomHashObject = new RandomHash (12345);
int randomNumber2 = randomHashObject.GetHash (2);
int randomNumber3 = randomHashObject.GetHash (3);
int randomNumber1 = randomHashObject.GetHash (1);
Хеш-функції можуть обробляти кілька вхідних значень, тобто, їх можна використовувати для певних 2D- або 3D-координат:
RandomHash randomHashObject = new RandomHash (12345);
randomNumberGrid [20, 40] = randomHashObject.GetHash (20, 40);
randomNumberGrid [21, 40] = randomHashObject.GetHash (21, 40);
randomNumberGrid [20, 41] = randomHashObject.GetHash (20, 41);
randomNumberGrid [21, 41] = randomHashObject.GetHash (21, 41);
Процедурна генерація - нетипове використання хеш-функцій, так що не всі вони будуть слушними, або видаючи погане розподіл, або вимагаючи невиправдано багато ресурсів.
Одна з традиційних областей застосувань хеш-функцій - реалізація структур даних, таких як словники. Найчастіше вони дуже швидкі, але абсолютно позбавлені елементу випадковості, тому що потрібні головним чином для більш ефективного виконання алгоритмів.
Інша область їх застосування - криптографія. Такі хеш-функції показують хорошу випадковість, але при цьому дуже повільні, тому що вимоги до криптографически стійким функцій набагато вище, ніж до значень, які тільки виглядають випадковими.
Нам потрібна хеш-функція, яка виглядає випадково, і в той же час ефективна, тобто не уповільнена нічим зайвим. В обраному вами мовою програмування такий може і не знайтися, так що доведеться підшукувати підходящу для впровадження в проект.
Я протестував кілька хеш-функцій, відібраних на основі рекомендацій з усіх куточків Інтернету. Для порівняння я вибрав три з них.
- PcgHash: Цю функцію мені порекомендував Адам Сміт (Adam Smith) на форумі Google Groups. Адам припустив, що навіть без особливих навичок не так вже й складно створити власну хеш-функцію і запропонував свій код PcgHash в якості прикладу.
- MD5: Це одна з найбільш відомих хеш-функцій. Вона використовується для криптографічних потреб і для наших цілей занадто витратна. До того ж, нам зазвичай потрібні 32-бітові цілі значення, тоді як MD5 повертає набагато більш об'ємні числа, велика частина яких буде відкидатися. Проте, її варто включити в порівняння.
- xxHash: Це сучасна високопродуктивна НЕ-криптографічний функція, що проявляє і хороші випадкові властивості, та відмінну швидкодію.
Для тестування поряд з побудовою «гучних» зображень і отрисовкой координат я також використовував ENT - Програму тестування псевдовипадкових Числових Послідовностей. Я додав до зображень обрані показники ENT і показник, який я сам винайшов і назвав «відхиленням діагоналей» - розглядаються суми діагональних ліній пікселів на відображенні координат і вимірюється стандартне відхилення цих сум.
Ось результати за трьома зазначеним функціям:

PcgHash різко виділяється: хоч вона і показує здається випадковим результат на галасливому зображенні, отрисовка координат виявляє чіткий візерунок, а значить, вона погано справляється з простими трансформаціями. З цього я можу зробити висновок, що створення власних хеш-функцій - справа нелегка, і його, мабуть, краще залишити професіоналам.
MD5 і xxHash показують хорошу випадковість, при цьому друга працює в 50 разів швидше.
Перевага xxHash ще й в тому, що навіть не будучи ГСЧ, вона зберігає концепцію сида, чого не скажеш про всі хеш-функціях. Можливість вказівки сида - явна перевага в області процедурної генерації, бо з різними сидами ви можете призначати різні випадкові властивості об'єктів, клітин або подібного, а потім просто використовувати індекс об'єкта / координати клітини в якості вхідного значення хеш-функції. Що особливо важливо - числа з послідовностей з різними сидами будуть випадковими по відношенню один до одного (подробиці в Додатку 2).
Оптимізація хеш-функцій для процедурної генерації
З проведених досліджень мені стало очевидно, що крім вибору функції, яка демонструє високу продуктивність в хеш-бенчмарках загального призначення, критично важливо оптимізувати її роботу під потреби процедурної генерації, не залишаючи функцію «як є».
Ось два основних способи оптимізації:
- Уникайте перетворень між цілими числами і байтами. Більшість хеш-функцій загального призначення беруть на вході масив байтів і видають ціле або кілька байтів в якості результату. Однак, деякі продуктивні функції переводять вхідні байти в цілі, тому що оперують цілими на внутрішньому рівні. Для процедурної генерації цілком природно отримувати результат хеш-функції на основі цілих входять значень, так що перетворення їх в байти безглуздо. Відмова від використання байтів може потроїти продуктивність, залишаючи результат ідентичним на 100%.
- Реалізація «бесціклічних» методів з одним або декількома вхідними значеннями. Більшість хеш-функцій загального призначення приймають вхідні дані змінної довжини в формі масиву. Це корисно і в процедурній генерації, але нам, як правило, потрібно результат на основі 1, 2 або 3 цілих чисел. Створення оптимізованих методів, які беруть фіксовану кількість значень замість масиву дозволяє усунути необхідність в циклі всередині функції, що різко підвищує продуктивність (в 4-5 разів, згідно з моїми тестам). Я не експерт в низкоуровневой оптимізації, але таку різницю можна домогтися або Неявним перетворенням в циклі for (C # / implicit - for loop має в собі умову, як мінімум одне, тому програма галузиться, нема циклу, немає проблем), або виділенням пам'яті під масив .
Мої поточні рекомендації зводяться до використання версії xxHash, оптимізованої для процедурної генерації. Детальніше дивіться в Додатку C.
Мої версії xxHash і інших хеш-функцій можна знайти на BitBucket . Вони написані на C #, але труднощів з портированием на інші мови виникнути не повинно.
Крім оптимізації, я додав кілька методів для отримання результату у вигляді цілого числа в заданому діапазоні або числа з плаваючою комою в заданому діапазоні, як зазвичай потрібно в процедурній генерації.
Примітка: на момент написання статті я додав тільки оптимізацію єдиного цілого на вході в xxHash і MurmurHash3. Як буде вільний час, додам оптимізацію з двома і трьома вхідними цілими значеннями.
Комбінування хеш-функцій і ГСЧ
Генератори випадкових чисел можна комбінувати з хеш-функціями. Розумний підхід полягає у використанні ГСЧ з різними сидами, але так, щоб сиди проходили через випадкову хеш-функцію, а не застосовувалися безпосередньо. Уявіть, що ваш світ - це величезний лабіринт, потенційно практично нескінченний. На величезній сітці території кожна клітина - лабіринт. Поки гравець пересувається по ігровому світу, лабіринти генеруються в найближчих клітинах.
Якщо ви хочете, щоб кожен відвіданих лабіринт залишався незмінним, вам потрібні випадкові значення, які базуються на попередніх з послідовності.
Однак, лабіринти генеруються по одному за раз, так що немає необхідності контролювати порядок випадкових чисел в кожному з них.
Ідеальним підходом буде використання випадкової хеш-функції для генерації сидов лабіринтів на основі їх координат і подальше використання сида для генерації послідовності випадкових чисел.
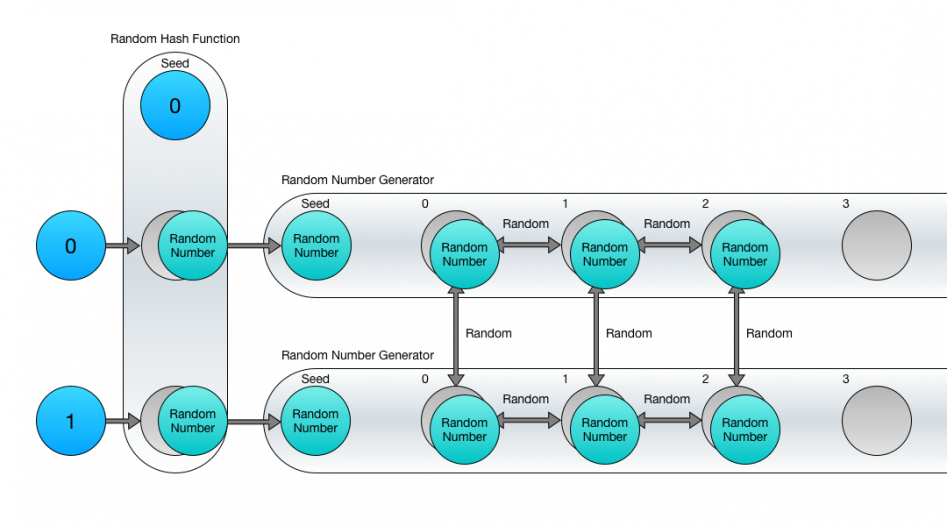
Код на C # буде виглядати приблизно так:
RandomHash randomHashObject = new RandomHash (12345);
int mazeSeed = randomHashObject.GetHash (cellCoord.x, cellCoord.y);
Random randomSequence = new Random (mazeSeed);
int randomNumber1 = randomSequence.Next ();
int randomNumber2 = randomSequence.Next ();
int randomNumber3 = randomSequence.Next ();
висновок
Якщо вам потрібен контроль над порядком випадкових чисел, використовуйте оптимізовану для процедурної генерації версію підходящої випадкової хеш-функції (таку як xxHash).
Якщо порядок випадкових чисел не важливий, найпростішим способом їх отримання буде ГСЧ, наприклад клас System.Random в C #. Якщо все числа повинні бути випадковими по відношенню один до одного, вони повинні входити в одну послідовність (ініціалізувала одним сідом), або сиди різних послідовностей повинні спочатку пропускатися через випадкову хеш-функцію.
Вихідний код вищезгаданої тестового середовища для випадкових чисел , Разом з різними ГСЧ і хеш-функціями, можна знайти на BitBucket.
Додаток A: Примітка з тривалого шуму
У деяких випадках вам можуть знадобитися тривалі значення шуму, тобто близькі за значенням вхідні дані, що дають близькі за значенням результати. Зазвичай використовуються для поверхні землі і текстур.
Така вимога кардинально відрізняється від розглянутого в статті. Для тривалих шумів звертайтеся до функції Perlin Noise або краще Simplex Noise.
Однако, Врахуй, что смороду підходять только для тріваліх шумів. Запит функцій трівалого шуму для Отримання Звичайно Випадкове чисел, Які НЕ пов'язані з іншімі, дасть погані результати, так як ЦІ алгоритми оптімізовані для других цілей. Наприклад, я помітив, що запит функції Simplex Noise по позиціях цілих чисел видає 0 кожен третій раз!
До того ж, функції тривалого шуму в своїх обчисленнях зазвичай використовують числа з плаваючою комою, стабільність і точність яких погіршуються разом з віддаленням від оригіналу.
Додаток B: Результати додаткових тестів
Протягом багатьох років я зустрічаюся з різними помилками і зараз спробую розібратися ще дещо з якими з них.
Чи не краще використовувати в якості сида великі значення?
Ні, я не помічав нічого, що б на це вказувало. Поглянувши на результати тестів в цій статті, ви побачите, що різниці між великими та маленькими значеннями немає.
ГСЧ потрібно зробити кілька значень, щоб «розігнатися»?
Ні, як ви бачите на тестових зображеннях, послідовності випадкових чисел слідують одному візерунку від початку (верхній лівий кут і далі рядок за рядком) до кінця.
На зображенні нижче я порівняв нульові числа з 65536 послідовностей з сотими числами з них же. Як бачите, помітної різниці між (поганим) якістю випадковості немає.

Правда, що деякі ГСЧ, наприклад в Java, видають кращу випадковість чисел з послідовностей з різними сидами?
Можливо, трішки краще, але вона все одно далека від прийнятної. На відміну від класу Random в C #, клас Random в Java злегка перемішує біти в сидах перед їх збереженням.
Підсумкові числа з різних послідовностей виглядають трохи більш випадковими і ми бачимо, що показник серійної кореляції набагато краще. Але на відображенні координат прекрасно видно, що дані, як і раніше вишиковуються в прямі лінії.

Насправді, я не бачу причин, за якими ГСЧ не використовують попередню обробку сидов високоякісної хеш-функцією. Це виглядає дійсно хорошою ідеєю без будь-яких недоліків. Просто відомі мені популярні ГСЧ цього не роблять, так що вам доведеться скористатися описаним мною способом і зробити все самостійно.
Чому для випадкових хеш-функцій можна використовувати різні сиди, а для ГСЧ не можна?
Немає ніякої внутрішньої причини, але такі хеш-функції, як xxHash і MurmurHash3 розглядають сид як вхідний значення, так би мовити, застосовуючи до Сіду високоякісну випадкову хеш-функцію. Завдяки такій реалізації завжди можна безпечно використовувати n-ну кількість з послідовності з іншим сідом.

Додаток C: Додаткове порівняння хеш-функцій
В оригінальній версії цієї статті я порівнював PcgHash, MD5, і MurmurHash3 і радив користуватися MurmurHash3. MurmurHash3 володіє чудовими властивостями випадковості, і пристойною швидкістю. Її автор також розробив середу тестування хеш-функцій SMHasher , Що набула широкого поширення.
Крім того, я звертався до цього питання на Stack Overflow , Де порівнюється безліч функцій і теж проглядається перевагу MurmurHash.
Після публікації Арас Пранкевічус (Aras Pranckevičius) порадив мені поглянути на xxHash , А Нейтан Рід (Nathan Reed) на Wang Hash, про яку він написав тут.
xxHash змогла перемогти MurmurHash на її рідному полі, показавши такі ж високі результати в SMHasher і при цьому демонструючи набагато більш високу продуктивність. Про xxHash можна почитати на її сторінці на Google Code .
Допрацьована мною версія після видалення перетворення байтів виявилася трохи швидше MurmurHash3, але далеко не настільки, як показано в результатах SMHasher.
Також я попрацював з WangHash. Якість випадковості виявилося недостатнім, як видно по проглядатися узорів на відображенні координат, але зате вона в п'ять разів швидше xxHash. Потім я відчув WangDoubleHash, згодовують собі свої результати, і її якість була відмінним та швидкість все ще втричі швидше xxHash.

Однак, WangHash (і WangDoubleHash) використовують на вході тільки одне ціле число, що спонукало мене створити подібні версії xxHash і MurmurHash3. Результат виявився вражаючим (4-5-кратне збільшення швидкості) - настільки, що xxHash зараз швидше WangDoubleHash.

Що стосується якості, моя тестового середовища показує помітні недоліки, але вона далеко не така складна, як SMHasher, а значить, високі результати в SMHasher дозволяють точніше судити про властивості випадковості, ніж мої власні тести. Я б сказав, що пройшли мою перевірку хеш-функції можна вважати ефективними для процедурної генерації, але якщо вже xxHash (в своїй оптимізованої формі) все одно якнайшвидша з усіх функцій, які пройшли мої тести, то я можу сміливо порекомендувати її.
Я б міг включити в порівняння та інші функції, але сумніваюся, що результати xxHash були б серйозно перевершені, тому поки що можу спокійно залишити все так, як є.
Оригінал знаходиться тут, A Primer on Repeatable Random Numbers .
Чи можу я просто використовувати ГСЧ з різними значеннями сида?ГСЧ потрібно зробити кілька значень, щоб «розігнатися»?
Правда, що деякі ГСЧ, наприклад в Java, видають кращу випадковість чисел з послідовностей з різними сидами?
Чому для випадкових хеш-функцій можна використовувати різні сиди, а для ГСЧ не можна?
Навіщо може знадобитися повторювати один і той же результат?
Навіщо мені може знадобитися конкретне число з послідовності?
Чи можу я просто використовувати ГСЧ з різними значеннями сида?
Так адже вони майже випадкові?
Цього ж буде досить?
Але навіщо?